✕
Request Demo

From The Ergoweb® Learning Center

Biomechanics

Dan MacLeod, CPE, MA, MPH


Biomechanics1Biomechanical models are mathematical predictive equations that can be used in this manner to estimate loads on the human body. These models can be complex, including the weight of the body and various orientations of the joints in question.Biomechanics is the study of the physical structure of living organisms. As related to workplace ergonomics, the human body is viewed as a system of levers. At the simplest level, by knowing the weight of a held object and the distance from a joint, the load on that joint can easily be calculated.

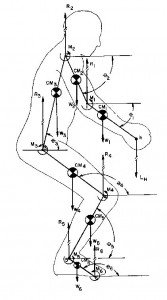
Biomechanics2 Biomechanics3

The University of Michigan Static Strength Prediction Program (more commonly known as the “Michigan 3D model”) is commercially available software. It is considered the gold standard for task assessment, although proprietary and somewhat complicated to use.

Simple back model

The University of Utah has developed simpler models that are publicly available, easy to use, and acceptably accurate compared with the Michigan 3D model. This approach uses the following variables:

BW = Body Weight (in pounds)
L = Load (in pounds)
HB = Hand to Back distance (in inches)
Cos(theta) = Torso angle from vertical:Torso posture — use:
Vertical 0
Bent 1/8 of the way .17
Bent 1/4 of the way .38
Bent 1/2 of the way .71
Bent 3/4 of the way .92
Bent horizontal 1.00		 Biomechanics4

The equation takes into account (A) back muscle force reacting to upper body weight, (B) back muscle force reacting to load, and (C) direct compressive component of upper body weight.

Compression force = A + B + C
A = 3(BW)cos(theta)
B = 0.5(L*HB)
C = 0.8[(BW)/2 +L]

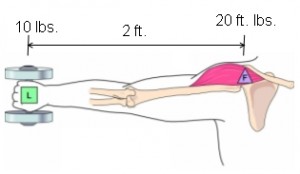
Simple shoulder model

The Utah model for estimating loads on the shoulder follows a similar pattern

BW = Body Weight (in pounds)
L = Load (in pounds, per hand)
HS = Horizontal distance from Hands to Shoulder (in inches)

The equation takes into account (A) moment at the shoulder due to the weight of the arm and (B) moment at the shoulder due to the weight of the load in the hands.

Moment = A + B
A = 0.0115 x BW x HS
B = L x HS

Note: For both models, Body Weight can be standardized at 160 lbs. to estimate effects on a general working population (160 lbs. = average weight mixed male/female population).